微积分II期中复习

级数

级数敛散性

p级数的敛散性

p级数$\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}$在$p>1$时收敛，$p\leq1$的时候发散
可以通过积分证明。此处不证

数项级数的基本性质

1. 线性运算法则（比较显然）
2. 改变一个级数的有限项不影响级数的敛散性
3. 若级数$\displaystyle \sum_{n=1}^{\infty}u_n$收敛，则在级数中任意添加括号得到的新级数也收敛且其和不变
4. 若级数$\displaystyle \sum_{n=1}^{\infty}u_n$收敛，则$\displaystyle \lim_{n\rightarrow\infty}u_n=0$

比较判别法

设$\displaystyle \sum_{n=1}^{\infty}u_n,\sum_{n=1}^{\infty}v_n$均为正项级数，且$u_n\leq v_n(n=1,2,3,...)$
（1）若$\displaystyle \sum_{n=1}^{\infty}v_n$收敛，则$\displaystyle \sum_{n=1}^{\infty}u_n$收敛
（2）若$\displaystyle \sum_{n=1}^{\infty}u_n$发散，则$\displaystyle \sum_{n=1}^{\infty}v_n$发散

比较判别法的极限形式

设$\displaystyle \sum_{n=1}^{\infty}u_n,\sum_{n=1}^{\infty}v_n$均为正项级数，且

$$\displaystyle \lim_{n\rightarrow\infty}\frac{u_n}{v_n}=l$$

（1）当$0<l<+\infty$时，两个级数的敛散性相同
（2）当$l=0$时，若$\displaystyle \sum_{n=1}^{\infty}v_n$收敛，则$\displaystyle \sum_{n=1}^{\infty}u_n$收敛
（3）当$l=+\infty$时，若$\displaystyle \sum_{n=1}^{\infty}v_n$发散，则$\displaystyle \sum_{n=1}^{\infty}u_n$发散

比值判别法

设$\displaystyle \sum_{n=1}^{\infty}u_n$是正项级数，并且

$$\displaystyle \lim_{n\rightarrow\infty}\frac{u_{n+1}}{u_{n}}=\gamma$$

（1）当$\gamma<1$时，级数收敛
（2）当$\gamma>1$时，级数发散
（3）当$\gamma=1$时，本判别法失效

根值判别法

设$\displaystyle \sum_{n=1}^{\infty}u_n$是正项级数，且

$$\displaystyle \lim_{n\rightarrow\infty}\sqrt[n]{u_n}=\gamma$$

（1）当$\gamma<1$时，级数收敛
（2）当$\gamma>1$时，级数发散
（3）当$\gamma=1$时，本判别法失效

积分判别法

设$f(x)$在$[1,+\infty]$上是非负且递减的连续函数，记$u_n=f(n),n=1,2,3...$则级数$\displaystyle \sum_{n=1}^{\infty}u_n$与反常积分$\displaystyle\int_{1}^{+\infty}f(x)dx$的敛散性相同

绝对收敛与条件收敛

如果$\displaystyle\sum^\infty_{n=1}|u_n|$收敛，则$\displaystyle\sum^\infty_{n=1}u_n$也收敛
（1）如果$\displaystyle\sum^\infty_{n=1}|u_n|$收敛，则称$\displaystyle\sum^\infty_{n=1}u_n$绝对收敛 （2）如果$\displaystyle\sum^\infty_{n=1}|u_n|$发散，但$\displaystyle\sum^\infty_{n=1}u_n$收敛，则称$\displaystyle\sum^\infty_{n=1}u_n$条件收敛

绝对值的比值判别法

设$\displaystyle \sum_{n=1}^{\infty}u_n$是一般级数，并且

$$\displaystyle \lim_{n\rightarrow\infty}\frac{\left|u_{n+1}\right|}{\left|u_{n}\right|}=\gamma$$

（1）当$\gamma<1$时，级数绝对收敛
（2）当$\gamma>1$时，级数发散
（3）当$\gamma=1$时，本判别法失效

绝对值的根值判别法

设$\displaystyle \sum_{n=1}^{\infty}u_n$是一般级数，且

$$\displaystyle \lim_{n\rightarrow\infty}\sqrt[n]{\left|u_n\right|}=\gamma$$

（1）当$\gamma<1$时，级数绝对收敛
（2）当$\gamma>1$时，级数发散
（3）当$\gamma=1$时，本判别法失效

莱布尼兹定理

若交错级数$\displaystyle \sum_{n=1}^{\infty}(-1)^{n-1}u_n$满足下列条件：
（1）$u_1\geq u_2\geq u_3\geq ...$
（2）$\displaystyle \lim_{n\rightarrow \infty}u_n=0$
则$\displaystyle \sum_{n=1}^{\infty}(-1)^{n-1}u_n$收敛且它的和$S\leq u_1$

幂级数

阿贝尔定理

如果级数$\displaystyle \sum_{n=0}^{\infty}a_nx^n$当$x=x_0(x_0\neq 0)$时收敛，那么适合不等式$\left|x\right|<\left|x_0\right|$的一切$x$使该幂级数绝对收敛.
反之，如果级数$\displaystyle \sum_{n=0}^{\infty}a_nx^n$当$x=x_0(x_0\neq 0)$时发散，那么适合不等式$\left|x\right|>\left|x_0\right|$的一切$x$使该幂级数发散.
证明： 设$x_0$使幂级数收敛，则根据级数收敛的必要条件，有

$$\displaystyle \lim_{n\rightarrow\infty}a_nx_0^n=0$$

于是存在一个常数$M$，使得

$$\left|a_nx_0^n\right|\leq M(n=0,1,2,...)$$

则$\left|a_nx^n\right|=\left|a_nx_0^n\cdot \frac{x^n}{x_0^n}\right|\leq M\left|\frac{x}{x_0}\right|^n$
当$\left|x\right|<\left|x_0\right|$时级数$\displaystyle \sum_{n=0}^\infty M\left|\frac{x}{x_0}\right|^n$收敛，所以级数$\displaystyle \sum_{n=0}^{\infty}a_nx^n$收敛。
定理的后半部分用反证法即可。设级数$\displaystyle \sum_{n=0}^{\infty}a_nx^n$当$x=x_0$时发散且存在$x_1$使得$\left|x_1\right|>\left|x_0\right|$且使级数收敛，则由定理前半部分可知$\left|x\right|<\left|x_1\right|$的一切$x$使该幂级数绝对收敛.即$x_0$使幂级数绝对收敛，矛盾。

收敛半径，收敛区间和收敛域

1. 收敛半径：使幂级数收敛的所有收敛点的上确界
2. 收敛区间：设收敛半径为$R$，则收敛区间为$(-R,R)$
3. 收敛域：收敛区间与收敛端点的并集

柯西-阿达马公式

设幂级数$\displaystyle \sum_{n=0}^\infty a_nx^n$，若

$$\displaystyle \lim_{n\rightarrow\infty}\frac{\left|a_n\right|}{\left|a_{n+1}\right|}=R$$

（1）当$0<R<+\infty$时，级数$\displaystyle \sum_{n=0}^\infty a_nx^n$在$(-R,R)$内绝对收敛，当$\left|x\right|>R$时发散
（2）当$R=0$时，级数$\displaystyle \sum_{n=0}^\infty a_nx^n$仅在$x=0$处收敛，在$x\neq 0$时发散
（3）当$R=+\infty$时，级数$\displaystyle \sum_{n=0}^\infty a_nx^n$在$R$上绝对收敛

根值公式

设幂级数$\displaystyle \sum_{n=0}^\infty a_nx^n$，若

$$\displaystyle \lim_{n\rightarrow\infty}\frac{1}{\sqrt[n]{\left|a_{n}\right|}}=R$$

（1）当$0<R<+\infty$时，级数$\displaystyle \sum_{n=0}^\infty a_nx^n$在$(-R,R)$内绝对收敛，当$\left|x\right|>R$时发散
（2）当$R=0$时，级数$\displaystyle \sum_{n=0}^\infty a_nx^n$仅在$x=0$处收敛，在$x\neq 0$时发散
（3）当$R=+\infty$时，级数$\displaystyle \sum_{n=0}^\infty a_nx^n$在$R$上绝对收敛

常见的麦克劳林展开

1.$\displaystyle\frac{1}{1-x}= \sum^{\infty}_{n=0}x^n,\left|x\right|<1$

性质

若幂级数$\displaystyle \sum_{n=0}^\infty a_nx^n$的收敛半径为$R(>0)$，则
（1）级数在收敛域上的和函数$S(x)$是连续函数 （2）幂级数在$(-R,R)$上逐项可微，微分后得到的幂级数与原级数有相同的收敛半径 （3）幂级数在$(-R,R)$上逐项可积，积分后得到的幂级数与原级数有相同的收敛半径

傅里叶级数

周期函数的傅里叶展开

（狄利克雷定理）如果$f(x)$是以$T=2l$为周期的周期函数，且$f(x)$在$[-l,l]$上逐段光滑，那么$f(x)$的傅里叶级数在任意点$x$处都收敛，并且收敛于$f(x)$在该点左右极限的平均值。

$$\frac{a_0}{2}+\displaystyle \sum^{\infty}_{n=1}\left(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac{n\pi x}{l}\right)=S(x)=\frac{f(x-0)+f(x+0)}{2},x\in R$$

其中

$$a_n=\displaystyle\frac{1}{l}\int^l_{-l}f(x)\cos\frac{n\pi x}{l}dx,n=0,1,2,...$$

$$b_n=\displaystyle\frac{1}{l}\int^l_{-l}f(x)\sin\frac{n\pi x}{l}dx,n=1,2,3,...$$

$[-l,l]$上的傅里叶展开

$$\frac{a_0}{2}+\displaystyle \sum^{\infty}_{n=1}\left(a_n\cos\frac{n\pi x}{l}+b_n\sin\frac{n\pi x}{l}\right)=S(x)=\frac{f(x-0)+f(x+0)}{2},x\in (-l,l)$$

其中

$$a_n=\displaystyle\frac{1}{l}\int^l_{-l}f(x)\cos\frac{n\pi x}{l}dx,n=0,1,2,...$$

$$b_n=\displaystyle\frac{1}{l}\int^l_{-l}f(x)\sin\frac{n\pi x}{l}dx,n=1,2,3,...$$

$[0,l]$上的傅里叶展开

1. 奇延拓（正弦展开）
   令

$$F(x)=\begin{cases} f(x),0<x \leq l\\ 0,x=0\\ -f(-x),-l\leq x < 0 \end{cases}$$

对其进行傅里叶展开
$f(x)$在$[0,l]$上的正弦展开为

$$\displaystyle \sum^{\infty}_{n=1}b_n\sin\frac{n\pi x}{l}=S(x)=\frac{f(x-0)+f(x+0)}{2},x\in (0,l)$$

其中

$$b_n=\displaystyle\frac{2}{l}\int^l_{0}f(x)\sin\frac{n\pi x}{l}dx,n=1,2,3,...$$

1. 偶延拓（余弦展开）
   令

$$F(x)=\begin{cases} f(x),0\leq x \leq l\\ f(-x),-l\leq x \leq 0 \end{cases}$$

对其进行傅里叶展开
$f(x)$在$[0,l]$上的余弦展开为

$$\frac{a_0}{2}+\displaystyle \sum^{\infty}_{n=1}a_n\cos\frac{n\pi x}{l}=S(x)=\frac{f(x-0)+f(x+0)}{2},x\in (0,l)$$

其中

$$a_n=\displaystyle\frac{2}{l}\int^l_{0}f(x)\cos\frac{n\pi x}{l}dx,n=0,1,2,...$$

矢量代数

矢量积

结合律

$$m(\mathbf{a}\times\mathbf{b})=(m\mathbf{a})\times \mathbf{b}=\mathbf{a}\times(m\mathbf{b})$$

分配率

$$\mathbf{a}\times(\mathbf{b}+\mathbf{c})=\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}\\ (\mathbf{a}+\mathbf{b})\times\mathbf{c}=\mathbf{a}\times\mathbf{c}+\mathbf{b}\times\mathbf{c}$$

混合积

平行六面体的体积

起点相同的矢量$\mathbf{a},\mathbf{b},\mathbf{c}$所确定的平行六面体体积为

$$|\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})|$$

三矢量共面

三矢量$\mathbf{a},\mathbf{b},\mathbf{c}$共面的充要条件是他们的混合积

$$\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=0$$

其实可以视作上面的特例。

改变顺序的结果

1. 顺次轮换，混合积不变，即

$$\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=\mathbf{b}\cdot(\mathbf{c}\times \mathbf{a})=\mathbf{c}\cdot(\mathbf{a}\times \mathbf{b})$$

2. 任意对调两矢量顺序，符号相反，即

$$\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=-\mathbf{a}\cdot(\mathbf{c}\times \mathbf{b})\\ \mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=-\mathbf{b}\cdot(\mathbf{a}\times \mathbf{c})\\ \mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=-\mathbf{c}\cdot(\mathbf{b}\times \mathbf{a})$$

二重矢积

$$\mathbf{a}\times(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\cdot \mathbf{c})\mathbf{b}-(\mathbf{c}\cdot \mathbf{b})\mathbf{a}$$

空间解析几何

球面方程

$$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$$

柱面方程

由一条动直线$L$沿一定曲线$\Gamma$平行移动形成的曲面，称为柱面.并称动直线$L$为该柱面的母线，称定曲面$\Gamma$为该柱面的准线

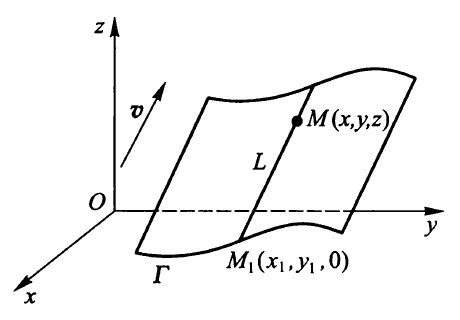
以$Oxy$平面的曲线$\Gamma:F(x,y)=0$为准线，母线$L$的方向矢量为$\mathbf{v}=a\mathbf{i}+b\mathbf{j}+c\mathbf{k}(c\neq0)$的柱面方程为

$$F(x-\frac{a}{c}z,y-\frac{b}{c}z)=0$$

证明：
设$M(x,y,z)$是柱面上一点，过$M$的母线与准线交于点$M_1$（如上图），$\overrightarrow{M_1M}//\mathbf{v}$，记$\overrightarrow{M_1M}=m\mathbf{v}$。而

$$\overrightarrow{M_1M}=(x-x_1)\mathbf{i}+(y-y_1)\mathbf{j}+(z-0)\mathbf{k}$$

可知$x-x_1=ma,y-y_1 =mb,z-0=mc$，消去$m$

$$x_1=x-\frac{a}{c}z,y_1=y-\frac{b}{c}z$$

由$F(x_1,y_1)=0$ 知柱面方程为$F(x-\frac{a}{c}z,y-\frac{b}{c}z)=0$

锥面方程

过空间一定点$O$的动直线$L$，沿空间曲线$\Gamma$（不过定点$O$）移动所生成的曲线称为锥面，其中动直线$L$称为该锥面的母线，曲线$\Gamma$称为该锥面的准线，定点$O$称为该锥面的顶点。

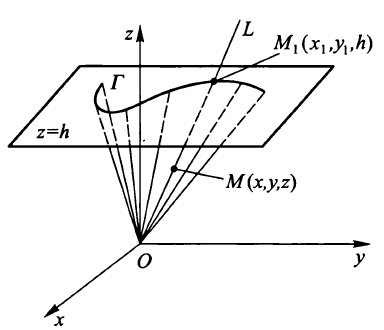
以$z=h(h\neq0)$平面上的曲线$\Gamma:F(x,y)=0$为准线，以原点为顶点的锥面方程为

$$F(\frac{h}{z}x,\frac{h}{z}y)=0$$

证明：
显然$\overrightarrow{OM}$与$\overrightarrow{OM_1}$共线，即$\overrightarrow{OM_1}=m\overrightarrow{OM}$

$$x_1=mx,y_1=my,h=mz$$

消去$m$,得到$x_1=\frac{h}{z}x,y_1=\frac{h}{z}y$
而$F(x_1,y_1)=0$
即曲面方程为$F(\frac{h}{z}x,\frac{h}{z}y)=0$

旋转曲面方程

一曲线$\Gamma$ 绕一定直线$L$旋转生成的曲面叫做旋转曲面，其中定直线L称为该旋转曲面的轴

平面上的曲线$\Gamma$绕坐标轴旋转所得的曲面方程

$Oyz$平面上的曲线$\Gamma:F(y,z)=0$绕$Oz$轴旋转一周得到的旋转曲面方程为

$$F(\pm\sqrt{x^2+y^2},z)=0$$

先写出平面上的曲线方程，然后根据轴决定替换其中哪个未知量，如本例中通过$Oyz$平面确定了曲线的方程应为$F(y,z)=0$，然后根据$Oz$轴确定$y$应被替换成$\sqrt{x^2+y^2}$

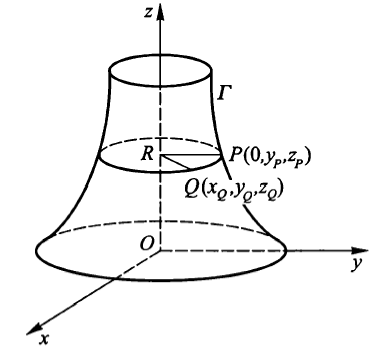
证明：
设$P(0,y_P,z_P)$是曲线$\Gamma$上任意一点，当曲线$\Gamma$绕$Oz$轴旋转一周时，点$P$的轨迹是一个圆，记圆心为$R$.设$Q(x_Q,y_Q,z_Q)$是这个圆上任意一点，则$z_P=z_Q$.

$$｜y_P｜=PR=QR=\sqrt{x_Q^2+y_Q^2}$$

将$y_P=\pm \sqrt{x_Q^2+y_Q^2},z_P=z_Q$代入$F(y_P,z_P)=0$ 得到曲面方程$F(\pm\sqrt{x^2+y^2},z)=0$

空间中任意直线绕坐标轴旋转所得的曲面方程

直线$\Gamma \begin{cases} x=x(t)\\ y=y(t)\\ z=z(t)\\ \end{cases}$绕$Oz$轴旋转生成的曲面方程为

$$x^2+y^2=[x(z^{-1}(z))]^2+[y(z^{-1}(z))]^2$$

证明：
设$M(x,y,z)$为所求曲面上的任一点，则$M$必是直线$\Gamma$上某个点$M_1(x_1,y_1,z_1)$绕$Oz$轴旋转某个角度得到的，即

$$\begin{cases} x_1=x(t_1)\\ y_1=y(t_1)\\ z_1=z(t_1)\\ \end{cases}$$

且$z=z_1,x^2+y^2=x_1^2+y_1^2$
由$z=z(t_1)$，知$t_1=z^{-1}(z)$,则

$$x_1=x[z^{-1}(z)],y_1=y[z^{-1}(z)]$$

所以旋转曲面方程为

$$x^2+y^2=[x(z^{-1}(z))]^2+[y(z^{-1}(z))]^2$$

多元函数微分学

多元函数的极限与连续性

若累次极限$\displaystyle \lim_{x\rightarrow x_0}\lim_{y\rightarrow y_0}f(x,y),\displaystyle \lim_{y\rightarrow y_0}\lim_{x\rightarrow x_0}f(x,y)$与二重极限$\displaystyle \lim_{(x,y)\rightarrow (x_0,y_0)}f(x,y)$都存在，则三者相等。

(2023 T5)求极限$\displaystyle \lim_{(x,y)\rightarrow (0,0)}x^2y\ln(x^2+y^2)$
解：
实际上，取$y=0$，我们会发现这个极限与$\displaystyle \lim_{x\rightarrow 0}x^2\ln x^2=0$相等，但是我们无法确定该极限存在，所以不能直接给出答案。
这种题目的通用做法是夹逼定理，为了去除正负的影响我们先取绝对值，也就是说我们需要证明

$$\displaystyle \lim_{(x,y)\rightarrow (0,0)}|x^2y\ln(x^2+y^2)|=0$$

我们想着化成$\displaystyle \lim_{x\rightarrow 0}x\ln x$的类似形式，因此有

$$0\leq|x^2y\ln(x^2+y^2)|\leq|x|\left|\frac{x^2+y^2}{2}\ln(x^2+y^2)\right|$$

$$\displaystyle \lim_{(x,y)\rightarrow (0.0)}|x|\left|\frac{x^2+y^2}{2}\ln(x^2+y^2)\right|=0\cdot 0 = 0$$

由夹逼定理，知

$$\displaystyle \lim_{(x,y)\rightarrow (0,0)}|x^2y\ln(x^2+y^2)|=0$$

也即

$$\displaystyle \lim_{(x,y)\rightarrow (0,0)}x^2y\ln(x^2+y^2)=0$$

偏导数

若函数$z=f(x,y)$的二阶偏导数$f''_{xy}(x,y),f''_{yx}(x,y)$都在点$P_0$处连续，则$f_{xy}''(x_0,y_0)=f_{yx}''(x_0,y_0)$
很多时候会写作

$$\frac{\partial ^2 z}{\partial x \partial y}=\frac{\partial ^2 z}{\partial y \partial x}$$

全微分

若二元函数$z=f(x,y)$在点$(x,y)$处的全增量$\Delta z = f(x+\Delta x,y+\Delta y)-f(x,y)$可以表示为

$$\Delta z = A\Delta x+ B \Delta y+o(\rho)(\rho = \sqrt{(\Delta x)^2+(\Delta y)^2}\rightarrow 0)$$

其中$A,B$与变量$x,y$的增量$\Delta x, \Delta y$无关，而仅与$x,y$有关，则称函数$f(x,y)$在点$(x,y)$处可微。其中

$$dz=A\Delta x+B\Delta y$$

称为函数$f(x,y)$在点$(x,y)$处的全微分，其中

$$A=f'_x(x,y),B=f'_y(x,y)$$

(2023 T7)设函数$f(x)=\begin{cases}\sqrt{|xy|}\sin\ln(x^2+y^2),(x,y)\neq(0,0)\\ 0,(x,y)=(0,0)\end{cases}$，求$f_x'(0,0),f_y'(0,0)$，并讨论$f$在点$(0,0)$处的可微性
解：

$$f_x'(0,0)=\displaystyle\lim_{x\rightarrow 0}\frac{f(x,0)-f(0,0)}{x}=\frac{0-0}{x}=0$$

$$f_y'(0,0)=\displaystyle\lim_{y\rightarrow 0}\frac{f(0,y)-f(0,0)}{y}=\frac{0-0}{y}=0$$

要验证函数在此点是否可微，只需看极限$\displaystyle \lim_{\Delta x \rightarrow 0 \atop \Delta y \rightarrow 0 }\frac{\Delta z-(A\Delta x+B\Delta y)}{\rho}$是否为0.

$$\displaystyle \lim_{\Delta x \rightarrow 0 \atop \Delta y \rightarrow 0 }\frac{\Delta z-(A\Delta x+B\Delta y)}{\rho}=\displaystyle \lim_{\Delta x \rightarrow 0 \atop \Delta y \rightarrow 0 }\frac{f(\Delta x,\Delta y)-f(0,0)-f_x'(0,0)\Delta x-f_y'(0,0)\Delta y}{\sqrt{(\Delta) x^2+(\Delta y)^2}}=\displaystyle \lim_{\Delta x \rightarrow 0 \atop \Delta y \rightarrow 0 }\frac{\sqrt{|\Delta x\Delta y|}\sin\ln((\Delta x)^2+(\Delta y)^2)}{\sqrt{(\Delta x)^2+(\Delta y)^2}}$$

若该极限存在，取$y=x$的方向趋于$(0,0)$点

$$\displaystyle \lim_{\Delta x \rightarrow 0 \atop \Delta y \rightarrow 0 }\frac{\sqrt{|\Delta x\Delta y|}\sin\ln((\Delta x)^2+(\Delta y)^2)}{\sqrt{(\Delta x)^2+(\Delta y)^2}}=\displaystyle \lim_{\Delta x \rightarrow 0 \atop \Delta y \rightarrow \Delta x }\frac{\sqrt{|\Delta x\Delta y|}\sin\ln((\Delta x)^2+(\Delta y)^2)}{\sqrt{(\Delta x)^2+(\Delta y)^2}}=\displaystyle \lim_{\Delta x \rightarrow0}\frac{\sin\ln 2(\Delta x)^2}{\sqrt{2}}$$

极限不存在，因此不可微。

复合函数的偏导数

若函数$u=\varphi(x,y),v=\psi(x,y)$在点$(x,y)$处的偏导数都存在，$z=f(u,v)$在点$(u,v)=(\varphi (x,y),\psi(x,y))$处可微，则复合函数$z=f[\phi(x,y),\psi(x,y)]$在点$(x,y)$处的偏导数存在

$$\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\cdot\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\cdot \frac{\partial v}{\partial x}$$

$$\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\cdot\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\cdot \frac{\partial v}{\partial y}$$

为简便起见，约定$f_1'$表示对第一个中间变量求偏导，$f_2'$表示对第二个中间变量求偏导，而$f''_{12}$表示先对第一个中间变量求偏导，再对第二个中间变量求偏导。

$$f''_{12}=f''_{21}$$

(2023 T8) 设$u=f(x,y)$有连续的二阶偏导数，引用新的自变量$s=x+y,t=x-y$化简方程

$$\frac{\partial^2u}{\partial x^2}-\frac{\partial^2u}{\partial y^2}+2\frac{\partial u}{\partial x}+2\frac{\partial u}{\partial y}=0$$

解：

$$\displaystyle\frac{\partial u}{\partial x}=\frac{\partial u}{\partial s}\cdot\frac{\partial s}{\partial x}+\frac{\partial u}{\partial t}\cdot\frac{\partial t}{\partial x}=\frac{\partial u}{\partial s}+\frac{\partial u}{\partial t}$$

$$\displaystyle\frac{\partial u}{\partial y}=\frac{\partial u}{\partial s}\cdot\frac{\partial s}{\partial y}+\frac{\partial u}{\partial t}\cdot\frac{\partial t}{\partial y}=\frac{\partial u}{\partial s}-\frac{\partial u}{\partial t}$$

$$\displaystyle\frac{\partial^2u}{\partial x^2}=\frac{\partial}{\partial x}(\frac{\partial u}{\partial x})=\frac{\partial}{\partial s}(\frac{\partial u}{\partial x})\cdot\frac{\partial s}{\partial x}+\frac{\partial}{\partial t}(\frac{\partial u}{\partial x})\cdot\frac{\partial t}{\partial x}=\frac{\partial}{\partial s}(\frac{\partial u}{\partial x})+\frac{\partial}{\partial t}(\frac{\partial u}{\partial x})=\frac{\partial^2 u}{\partial s^2}+\frac{\partial^2 u}{\partial s \partial t}+\frac{\partial^2 u}{\partial t \partial s}+\frac{\partial^2 u}{\partial t^2}=\frac{\partial^2 u}{\partial s^2}+2\frac{\partial^2 u}{\partial s \partial t}+\frac{\partial^2 u}{\partial t^2}$$

$$\displaystyle\frac{\partial^2u}{\partial y^2}=\frac{\partial}{\partial y}(\frac{\partial u}{\partial y})=\frac{\partial}{\partial s}(\frac{\partial u}{\partial y})\cdot\frac{\partial s}{\partial y}+\frac{\partial}{\partial t}(\frac{\partial u}{\partial y})\cdot\frac{\partial t}{\partial y}=\frac{\partial}{\partial s}(\frac{\partial u}{\partial y})-\frac{\partial}{\partial t}(\frac{\partial u}{\partial y})=\frac{\partial^2 u}{\partial s^2}-\frac{\partial^2 u}{\partial s \partial t}-\frac{\partial^2 u}{\partial t \partial s}+\frac{\partial^2 u}{\partial t^2}=\frac{\partial^2 u}{\partial s^2}-2\frac{\partial^2 u}{\partial s \partial t}+\frac{\partial^2 u}{\partial t^2}$$

全部代入原方程得到

$$\displaystyle \frac{\partial^2 u}{\partial s \partial t}+\frac{\partial u}{\partial s}=0$$

复合函数的全微分

多元函数具有一阶微分形式不变性。
若以$x,y$为自变量的函数$z=f(x,y)$可微，则有

$$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$$

若以$s,t$为自变量的函数$z=f(x,y)$和$x=x(s,t),y=y(s,t)$都有连续的偏导数，则$z$可微，且

$$dz=\frac{\partial z}{\partial s}ds+\frac{\partial z}{\partial t}dt$$

$$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$$